Advanced Field Epi:Manual 2 - Diagnostic Tests/en: Perbedaan revisi
(Importing a new version from external source) |
(Importing a new version from external source) |
||
| Baris 381: | Baris 381: | ||
|- | |- | ||
| − | | style="border:none;padding-top:0cm;padding-bottom:0cm;padding-left:0.191cm;padding-right:0.191cm;"| | + | | style="border:none;padding-top:0cm;padding-bottom:0cm;padding-left:0.191cm;padding-right:0.191cm;"| >0.8 - 1 |
| style="border:none;padding-top:0cm;padding-bottom:0cm;padding-left:0.191cm;padding-right:0.191cm;"| Excellent agreement | | style="border:none;padding-top:0cm;padding-bottom:0cm;padding-left:0.191cm;padding-right:0.191cm;"| Excellent agreement | ||
Revisi per 10 Mei 2015 14.30
Daftar isi
- 1 Pengujian diagnostik
- 1.1 Measures of diagnostic test performance
- 1.2 Measuring agreement between tests
- 1.3 Estimation of true prevalence from apparent prevalence
- 1.4 Group (aggregate) diagnostic tests
- 1.5 Estimating test sensitivity and specificity
- 1.6 References – diagnostic testing
Pengujian diagnostik
Dalam epidemiologi lapangan istilah diagnosis biasanya berarti identifikasi suatu penyakit atau suatu kondisi yang mempengaruhi hewan. Pengujian diagnostik merupakan suatu prosedur atau proces yang dapat mempengaruhi pengembangan suatu diagnosis. Istilah pengujian diagnostik dapat digunakan untuk merujuk pada pemeriksaan klinis terhadap hewan atau pengujian laboratorium yang dilakukan pada sampel yang dikumpulkan dari hewan (darah, kotoran, dll). Hasil pengujian kemudian diterjemahkan dan digunakan untuk menentukan apakah hewan tersebut sakit atau tidak.
Diagnostic tests may be applied to an individual animal (as above) or to a group or aggregate of animals such as a mob, herd or farm. The presence of one or more disease-positive animals in a mob may mean that the mob is declared infected (mob-level diagnosis).
Measures of diagnostic test performance
Accuracy and precision
Accuracy relates to the ability of the test to provide a result that is close to the truth (the true value). Accuracy is generally assessed in the long run, meaning that it can be thought of as the average of multiple test results. A test is therefore considered to be accurate when the average of repeated tests is close to the true value. Any one test result may itself not be as accurate as the average of repeated tests performed on the same sample.
Precision refers to how repeatable the test is. If the test is repeated and the result from different runs is always the same then the test is precise (regardless of whether the result is accurate or not).
In general, the greater the number of tests involved, the greater the increase in sensitivity or specificity, depending on the method of interpretation that is used.
Sensitivity and specificity for multiple tests
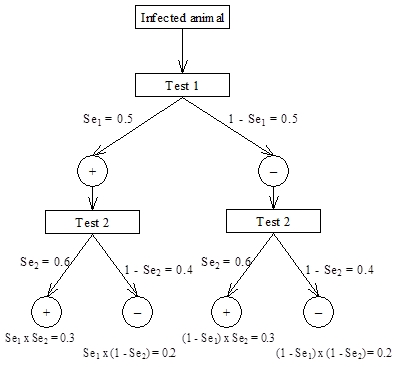
Overall values for sensitivity for interpretation of tests in series or parallel, assuming conditional independence of the tests, can be calculated using the following example.
For this example the two tests are assumed to be independent and have the following characteristics:
Test 1 - Se = 50%; Sp = 98.7% Test 2 - Se = 60%; Sp = 98.6%
What are the theoretical sensitivities and specificities of the two tests used in parallel or series?
For sensitivity, we assume an animal is infected and that it is tested with both Test 1 and Test 2. For Test 1, the probability of a positive test result (given that the animal is infected) is Se1 = 0.5 and the corresponding probability that it will give a negative result is 1 – Se1, also = 0.5 for this example. For Test 2, the probability of a positive test result (given that the animal is infected) is Se2 = 0.6 and the corresponding probability that it will give a negative result is 1 – Se2 = 0.4.
For series interpretation, both tests must be positive for it to be considered a positive result. From the scenario tree this is the result for the first limb on the left, which has probability P(+/+) = Se1 ï‚´ Se2 = 0.5 ï‚´ 0.6 = 0.3. Thus, the formula for sensitivity for series interpretation is Seseries = Se1 ï‚´ Se2 and for this example is 0.3 or 30%.
For parallel interpretation, the result is considered positive if either of the individual test results is positive. Alternatively, for a result to be considered negative both test results must be negative. Again this can be determined from the scenario tree, where the limb on the right represents both tests having a negative result and the probability of both negative results is P(–/–) = (1 – Se1)  (1 – Se2). Therefore the probability of an overall positive result for parallel interpretation is Separallel = 1 – (1 – Se1)  (1 – Se2) = 0.8 (80%) for this example.
Similar logic can be applied to the example of an uninfected animal to derive formulae for specificity for series and parallel interpretation as shown below:
Spparallel = Sp1 ï‚´ Sp2 = 0.973 or 97.3% for this example and
Spseries = 1 – (1 – Sp1)  (1 – Sp2) = 0.999 or 99.9% for our example
Figure 4.4: Scenario tree for calculating overall sensitivity for two tests interpreted in series or parallel
Conditional independence of tests
An important assumption of series and parallel interpretation of tests is that the tests being considered are conditionally independent. Conditional independence means that test sensitivity (specificity) remains the same regardless of the result of the comparison test, depending on the infection status of the individual.
If the assumption of conditional independence is violated then combined sensitivity (or specificity) will be biased. The "conditional" term relates to the fact that the independence (or lack of independence) is conditional on the disease status of the animal. Therefore sensitivities may be conditionally independent (or not) in diseased animals, while specificities may be conditionally independent (or not) in non-diseased animals.
Two tests are conditionally independent if test sensitivity or specificity (depending on disease status) of one test remains the same regardless of the result of the other (comparison) test
If tests are not independent (are correlated), the overall sensitivity or specificity improvements may not be as good as the theoretical estimates, because two tests will tend to give similar results on samples from the same animal.
For example, let us assume that the two tests described above were applied to 200 infected and 7,800 uninfected animals with the following results. What are the actual sensitivities and specificities for parallel and series interpretations and how do they compare to the theoretical values?
| 30 | 70 | ||
| 50 | 80 | ||
| 70 | 30 | ||
| 50 | 7620 | ||
| 200 | 7800 |
Observed sensitivities and specificities of the two tests used in parallel or series are:
| Seseries = 70/200 = 35% | Separallel = 150/200 = 75% |
| Spseries = 7770/7800 = 99.6% | Spparallel = 7620/7800 = 97.7% |
Sensitivity in series has dropped less than predicted (35% instead of 30% predicted), and sensitivity of parallel testing has increased less than predicted (75% compared to 80% predicted). The apparent difference between calculated and observed values for combined sensitivities suggests that these tests are in fact correlated.
This difference is due to correlation of the test sensitivities, so that infected animals that are positive to Test 1 are also more likely to be positive in Test 2, as shown by the substantial difference in sensitivity of Test 2 in animals positive to Test 1 (70/100 or 70%) compared to those negative to Test 1 (30/100 or 30%).
The differences in observed and predicted specificities are much smaller and in this case probably due to random variation.
Lack of conditional independence of tests is particularly likely if two tests are measuring the same (or similar outcome).
For example: ELISA and AGID are two serological tests for Johne’s disease in sheep. Both tests measure antibody levels in serum. Therefore, in an infected animal, the ELISA is more likely to be positive in AGID-positive animals than in AGID-negative animals, so that the sensitivities of the two tests are correlated (not independent). This is illustrated in Table xx.5, where the sensitivities of both tests vary markedly, depending on the result of the other test. In contrast, serological tests such as ELISA and AGID are likely to be less correlated with agent-detection tests, such as faecal culture.
| AGID | |||
| + | |||
| - | |||
| Total | |||
All 224 sheep are infected, so we can calculate sensitivities of both ELISA and AGID as follows:
Application of series and parallel testing
Series testing is commonly used to improve the specificity, and hence the positive predictive value, of a testing regimen (at the expense of reduced sensitivity).
For example, in large-scale screening programs, such as for disease control or eradication, a relatively cheap, high-throughput test with relatively high sensitivity and precision but only only modest specificity may be used for initial screening. This sort of test can be applied to large numbers of animals (entire population) where the purpose is to be very confident that those animals that test negative are in fact disease free.
Any positives to the initial screening test are then tested using a highly specific (and usually more expensive) confirmatory test to minimise the overall number of false positives at the end of the testing process. For an animal to be considered positive it must be positive to both the initial screening test and the confirmatory follow-up test.
A good example of series testing is in eradication programs for bovine tuberculosis, where the initial screening test is often either a caudal fold or comparative cervical intradermal tuberculin test, which is followed up in any positives by a range of possible tests including additional skin tests, a gamma interferon immunological test or even euthanasia and lymph node culture, depending on circumstances.
In the above situation it is important to realise that even though the follow-up test is only applied to those that are positive on the first test, this is still an example of series interpretation. Because an animal must test positive to both tests for a positive overall result, the result of the second test in animals negative to the first test is irrelevant, so that the test doesn’t actually need to be done. This is an important consideration in control or eradication programs, where testing costs are usually a major budget constraint and significant savings can be made by using a cheap, high-throughput screening test followed by a more expensive but highly specific follow-up test.
Parallel testing is less commonly used, but is primarily directed at improving overall sensitivity and hence negative predictive value of the testing regimen. Parallel testing is mainly applied where minimising false negatives is imperative, for example in public health programs or for zoonoses, where the consequences of failing to detect a case can be extremely serious. In contrast to series testing, every sample must be tested with both tests for parallel testing to be effective, so that testing costs can be quite high.
For example, in some countries testing for highly pathogenic avian influenza virus may rely on using a combination of virus isolation and PCR for detection of virus, with birds that are positive to either test being considered infected.
Measuring agreement between tests
There is often interest in comparing the diagnostic performance of two tests (new test compared to an existing test) to see if the new test produces similar results.
For the same specimens submitted to each of the two tests, the investigator records the appropriate frequency data into the 4 cells of a 2x2 table, a (both tests positive), b (test 1 positive and test 2 negative), c (test 1 negative and test 2 positive), and d (both tests negative). The value kappa (k), a measure of relative agreement beyond chance, can then be calculated using software such as EpiTools or using formulae in standard epidemiology texts.
Kappa has many similarities to a correlation coefficient and is interpreted along similar lines. It can have values between -1 and +1. Suggested criteria for evaluating agreement are (Everitt, 1989, cited by Thrusfield, 1995):
Table 4.: Table showing interpretation of kappa values
| kappa | Evaluation |
| >0.8 - 1 | Excellent agreement |
| >0.6 - 0.8 | Substantial agreement |
| Moderate agreement | |
| Fair agreement | |
| >0 - 0.2 | Slight agreement |
| 0 | Poor agreement |
| <0 | Disagreement |
Care must be taken in interpreting kappa - if two tests agree well, they could be equally good or equally bad! However, it may be possible to justify use of a newly developed test if it agrees well with a standard test and if it is cheaper to run in the laboratory.
Conversely, if two tests disagree, one test is likely to be better than the other although there may no way to tell which is better! The exception to this is where both tests have close to 100% specificity (i.e. no or few false positives). In this case the test with the larger number of positive results is likely to be more sensitive. McNemar’s Chi-squared test for paired data can also be used to test for significant differences between the discordant cells (b & c).
An example of kappa and agreement between tests
A comparison of two herd-tests for Johne’s disease in sheep yields the following results (from Sergeant et al., ([#_ENREF_18 2002])):
| Test 1 results | Total | ||
| 95 | |||
| 201 | |||
| Total | 296 | ||
How well do the two tests agree, and can you determine which test is better?
For these tests, kappa is 0.64, suggesting moderate-substantial agreement. However, McNemar’s chi-squared is 22.88, with 1 degree of freedom and P < 0.001. This means that the discordant cells (37 and 5) are significantly different. From the data available it is not possible to say which test is better – the additional positives on Test 1 could be either true or false positives, depending on test specificity.
In this case, Test 1 was pooled faecal culture (specificity assumed to be 100%) and Test 2 was the agar gel-diffusion test with follow-up of positives by autopsy and histopathology (specificity also assumed to be 100%). How does this change the assessment of the two tests?
Considering that both tests have specificity equal (or very close) to 100%, there are likely to be very few false-positives. Therefore it appears that the sensitivity of Test 1 (pooled faecal culture) is considerably higher than that for Test 2 (serology), since Test 1 detected a greater number of positives overall.
Proportional agreement of positive and negative results
In some circumstances, particularly where the marginal totals of the 2-by-2 table are not balanced, kappa is not always a good measure of the true level of agreement between two tests ([#6 Feinstein and Cicchetti, 1990]). For example, in the first example above, kappa was only 0.74, compared to an overall proportion of agreement of 0.94 In these situations, the proportions of positive and negative agreement have been proposed as useful alternatives to kappa ([#3 Cicchetti and Feinstein, 1990]). For this example, the proportion of positive agreement was 0.78, compared to 0.96 for the proportion of negative agreement, suggesting that the main area of disagreement between the tests is in positive results and that agreement among negatives is very high.
Estimation of true prevalence from apparent prevalence
When we apply a test in a population, the proportion of positive results observed is the apparent prevalence. However, depending on test performance, apparent prevalence may not be a good indicator of the true level of disease in the population (the true prevalence). However, if we can estimate the sensitivity and specificity of the test, we can also estimate the true prevalence from the apparent (test-positive) prevalence (AP) using the formula ([#16 Rogan and Gladen, 1978]):
| True prevalence = | AP + Sp - 1 |
| Se + Sp - 1 |
which has a solution for situations other than when Se + Sp = 1. All values are expressed as proportions (between 0 and 1) rather than percentages for these calculations. Confidence limits can be calculated for the estimate using a variety of methods implemented in EpiTools. When true prevalence is 0, apparent prevalence = 1 - Sp, the false positive test rate.
For example: Say we have conducted a survey with a test whose sensitivity is 90% (0.9) and specificity is 95% (0.95) and we find a reactor rate (apparent prevalence) of 15% (0.15). By using the formula, we can estimate the true prevalence to be 11.8% (0.118).
Another example
Suppose we have conducted a survey of white spot disease in a shrimp farm, using a test with sensitivity of 80% (0.8) and specificity of 100% (1.0). We have tested 150 shrimp, and 6 shrimp tested positive. What is the estimated true prevalence?
The apparent prevalence is 6/150 = 0.04 or 4% (Wilson 95% CI: 1.8% - 8.5%)
Therefore, true prevalence = (0.04 + 1 - 1)/(0.8 + 1 - 1) = 0.04/0.8 = 0.05 or 5% (95% CI: 1.1 - 8.9%)
What happens if we assume that sensitivity and specificity are both 90%?
If Se = 0.9 and Sp = 0.9:
Therefore, true prevalence = (0.04 + 0.9 – 1)/(0.9 + 0.9 – 1) = –0.06/0.8 = –0.0625.
The above example illustrates one potential problem with Rogan and Gladen formula, which is that in some circumstances negative estimates can be produced. However, a negative (<0) prevalence is clearly impossible, so for this scenario the assumptions about sensitivity and specificity must be incorrect. For example, if specificity was 90% (0.9), and you tested 150 animals, you would expect to have 0.1*150 or on average about 15 false positive results (even in an uninfected population). Therefore if only 4 positives were recorded, the specificity of the test must be much higher than 90% (a minimum estimate would be to assume all of the positives are false positives, so that specificity = 1 - apparent prevalence = 1 - 4% or 96%).
Because prevalence estimates are proportions we should also calculate and present confidence intervals for the estimate.
Group (aggregate) diagnostic tests
The previous discussion describes the testing of individual animals. However, in epidemiological investigations, the study unit can often comprise a group of animals such as a herd of cattle, a flock of sheep, or a cage or pond of fish. For example, it is common practice to determine herd or flock status for some diseases based on the results of testing of a sample of animals, rather than testing the whole herd or flock.
In this situation, it is important to realise that testing for disease at the group or aggregate level incorporates a number of factors additional to those relevant to testing at the individual animal level. Thus, tests which may be highly sensitive and specific at the individual animal level can still result in misclassification of a high proportion of groups where only a small number of animals in each group are tested.
At the individual animal level, diagnostic test performance is determined by its sensitivity and specificity. The corresponding group-level measures are herd sensitivity and herd specificity. Herd sensitivity and herd specificity are affected by animal-level sensitivity and specificity, as well as the number of animals tested, the prevalence of disease in the group and the number of individual animal positive results (1, 2, 3 etc) used to classify the group as positive. Just as we do for individuals, we also want high sensitivity and high specificity in our group level interpretation.
Herd sensitivity (SeH) is the probability that an infected herd will give a positive result to a particular testing protocol, given that it is infected at a prevalence equal to or greater than the specified design prevalence.
Herd specificity (SpH) is the probability that an uninfected herd will give a negative result to a particular testing protocol (HSP)
Calculating herd sensitivity and herd specificity
The herd-level sensitivity (SeH) and specificity (SpH) with a cut-off of 1 reactor to declare a herd infected can be calculated as ([#13 Martin et al., 1992]):
SeH = 1 - (1 - (Prev x Se + (1 - Prev) x (1-Sp)))m and
SpH = Spm
Where Se and Sp are animal-level sensitivity and specificity respectively, Prev is true disease prevalence and m is the number of animals tested. SeH is equivalent to the level of confidence of detecting infection in herds or flocks with the specified prevalence of infection. SeH and SpH can be easily calculated using EpiTools or other epidemiological calculators.
If test specificity is 100% (i.e. any reactors are followed up to confirm their status) calculation of SeH is simplified:
SeH = 1 - (1 - Prev</nowiki> x Se)m
An example
For example, assuming that we have tested 100 animals in a herd with a test that has Se = 0.9 and Sp = 0.99, what is the herd-sensitivity for an assumed prevalence of 5%?
SeH = 1 - (1 - (0.05*0.9 + (1 - 0.05)*(1 - 0.99)))100
= 0.996 or 99.6%
This means that if disease is present at a prevalence of 5% or more, there is a 99.6% chance that one or more animals in the sample will test positively.
For this scenario, herd-specificity is:
SpH = 0.99100 = 0.37 or 37%
This means that there is a 37% chance that an uninfected herd will also have one or more animals test positively.
What happens if we assume that the prevalence of infection is 2% instead of 5%?
Herd-sensitivity:
SeH = 1 – (1 – (0.02*0.9 + (1 – 0.02)*(1 – 0.99)))100
= 0.94 or 94%
SeH decreases as prevalence decreases.
Herd-specificity:
SpH = 0.99100
= 0.37 or 37%
SpH is unaffected by prevalence because, by definition, SpH applies only to herds with zero prevalence (uninfected).
In the above example, increasing the cut-point number of reactors for a positive result from 1 to 2 (i.e. if there are 0 or 1 animals test positive the group is considered "uninfected" while if 2 or more test positive it is infected) results in an increase in SpH to 74% but a reduction in SeH to 77% (from EpiTools: http://epitools.ausvet.com.au/content.php?page=HerdSens3).
The formulae above assume that sample size is small relative to population size (or that the population is large). Similar formulae are also available for small populations or where the sample size is large relative to population size.
Risk of infection in test-negative animals
The only way to be 100% confident that no animals comprising a particular group are infected with a particular agent is to test every animal in the group with a diagnostic test which has perfect sensitivity and specificity. However, if only a low proportion of individual animals in the group are infected and only a small number are tested there can be quite a high chance that infected groups will be misclassified as uninfected. The following table shows the number of infected animals which may be present but undetected in a population of 100,000, despite a sample testing negative using a test with perfect sensitivity and specificity at the individual animal level.
Table 4.3: Number of diseased or infected animals which could remain in a group of 100,000 after a small number are tested and found to be negative using a test which has perfect sensitivity and specificity at the individual animal level for 95% and 99% confidence levels
| No. of animals in sample tested from group of 100,000 and found negative | ||
The situation is further complicated where the test procedure being used has poor sensitivity, which is the case for many tests in regular use.
The probability of introducing infection in a group of tested-negative animals is the same as the probability that one or more animals in the group are infected but tests negative. This probability can be calculated as:
| Probability | = 1 - NPVm |
| = 1 - [(1-Prev) x Sp/((1-Prev) x Sp + Prev x (1-Se))]m |
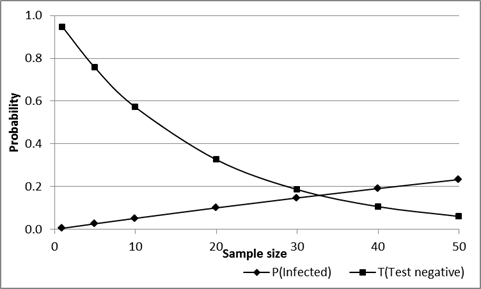
Where NPV is the negative predictive value of the test in the population of origin, Se and Sp are animal-level sensitivity and specificity respectively, Prev is true disease prevalence and m is the number of animals tested. As sample size increases the probability that the group will all test negative decreases, so that the overall risk associated with a group can be reduced by increasing the sample size. However, if all animals do test negatively the probability that one or more are actually infected increases (assuming that they are from an infected population), as shown in Figure 4.6.
For example: If 20 animals are selected from a herd or flock with a true prevalence of 0.05 (5%) and are tested using a test with Se=0.9 and Sp=0.99, and all 20 have a negative result, the probability that there are one or more infected animals in the group is about 0.1 (10%). In addition, the probability that all 20 animals will have a negative test result is about 0.33 (33%).
In simple language, there is a 1 in 3 chance that all animals test negative and also a 1 in 10 chance that there is one or more infected animals in the group, even if they have all tested negative.
Increasing sample size from 20 to 40 reduces the probability that all will test negatively from 33% to about 10%, but for those that are all negative, increases the probability that one or more are infected from 10% to 20% (1 in 5).
Figure 4.: Effect of sample size on the probability that a group of test-negative animals will include one or more infected (but test-negative) animals, and the probability that this will occur, for an assumed Se=0.9, Sp-0.99 and true prevalence=0.05 (5%) in the herd/flock of origin.
Demonstrate freedom of detecting disease?
It is impossible to prove that a population is free from a particular disease without testing every individual with a perfect test. However, demonstrating "freedom" from disease in a population is essentially the same as sampling to provide a high level of confidence of detecting disease at specified (design) prevalence. If we don't detect disease, then we can state that we have the appropriate level of confidence that (if the disease is present) it is at prevalence lower than the design prevalence. Provided we have selected appropriate design prevalence, it can then be argued that if the disease were present it would more than likely be at a higher level than the design prevalence, and therefore we can be confident that the population is probably free of the disease.
The selection of appropriate design prevalence is obviously critical if it is too low sample sizes will be excessive, while if it is too high the argument that it is an appropriate threshold for detection of disease is weaker. For infectious diseases it is common to use a value equal to or lower than values observes in endemic or outbreak situations.
Important factors to consider in group testing
When testing a group of animals for the presence of disease, there are a number of important points to keep in mind:
- Individual and group level test characteristics (sensitivity and specificity) are not equivalent.
- The number of animals to be tested in the group (sample size) is relatively independent of group size except for small groups (<~1000) or where sample size is more than about 10% of the group size. Alternative methods are available for small populations or where sample size is large relative to group size.
- The number of animals required to be tested in the group depends much more on individual animal specificity than it does on sensitivity.
- The number of animals to be tested in the group is linearly and inversely related to the expected prevalence of infected animals in the group.
- As the required level of statistical confidence increases, so the required sample size increases. The usual level is 95%. If this is increased to 99%, there is an approximate increase of 50% in the required sample size. For a reduction from 95% to 90% confidence, there is a decrease in sample size by 25%.
- As the sample size increases, group level sensitivity increases.
- As the number of animals used to classify the group as positive is increased, there is a corresponding increase in specificity.
- As group level sensitivity increases, group level specificity decreases.
- When specificity = 100% at the individual animal level, all uninfected groups are correctly classified i.e. group level specificity also equals 100%.
Estimating test sensitivity and specificity
There are two broad approaches to estimating test sensitivities and specificities.
"Gold standard" methods rely on the classification of individuals using a reference test (or tests) with perfect sensitivity and/or specificity to identify groups of diseased and non-diseased individuals in which the test can be evaluated. In contrast, "Non-gold-standard" methods are used in situations where determination of the true infection status of each individual is not possible or economically feasible.
Regardless of the methods used for estimating sensitivity and specificity, a number of important principles must be considered when evaluating tests, as for any other epidemiological study ([#_ENREF_8 Greiner and Gardner, 2000]):
- The study population from which the sample is drawn should be representative of the population in which the test is to be applied;
- The sample of individuals to which the test is applied must be selected in a manner to ensure that it is representative of the study population;
- The sample should include animals in all stages of the infection/disease process;
- The sample size must be sufficient to provide adequate precision (confidence limits) about the estimate; and
- Testing should be undertaken with blinding as to the true status of the individual and to other test results.
Gold-standard methods
Gold standard methods have the advantage of using a known disease status as the reference test. This allows for relatively simple calculations to estimate sensitivity and specificity of the test being evaluated, using a simple two-by-two cross-tabulation of the test against disease status. However, for many conditions a gold-standard test either does not exist or is prohibitively expensive to use (for example may require slaughter and detailed examination and testing of multiple tissues for a definitive result). In such cases the best available test is often used as if it were a gold standard, resulting in biased estimates of sensitivity and specificity. Alternatively, it may only be possible to use a small sample size due to financial limitations or the nature of the disease, resulting in imprecise estimates.
Gold standard test evaluation assumes comparison with the true disease status of an animal based on the results of a test (or tests) with perfect sensitivity and/or specificity
For example: The "gold-standard" test for bovine spongiform encephalopathy (BSE) is the demonstration of typical histological lesions in the brain of affected animals. However, false-negative results on histology will occur in animals in an early stage of infection. Therefore, if a screening test is evaluated by comparison with histology, specificity will be underestimated because some infected animals could react to the screening test but be histologically negative, resulting in mis-classification as false-positives. In addition, any infected but histologically-negative animals that are negative on the screening test will be mis-classified as true-negatives, resulting in over-estimation of the sensitivity.
If a disease is rare, or if the "gold standard" test is complex and expensive to perform, sample sizes for estimation of sensitivity are likely to be small, leading to imprecise estimates of sensitivity. If a disease does not occur in a country it is impossible to estimate sensitivity in a sample that is representative of the population in which it is to be applied. Conversely, if a disease does not occur in a country or region, it is relatively easy to estimate test specificity, based on a representative sample of animals from the population, because if the population is free of disease all animals in the population must also be disease-free.
Sometimes a new test may appear to be more sensitive (or specific) than the existing “gold standard†test (for example, new DNA-based tests compared to conventional culture). In this situation, the new test will find more (or fewer) positives than the reference test and careful analysis is required to determine whether this is because it is more sensitive or less specific. Even then, it is often not possible to reliably estimate sensitivity or specificity because there is no fixed reference point, so it may only be possible to say that the new test is more sensitive (or specific) than the old test, without specifying a value.
Gold-standard methods for estimating sensitivity and specificity of diagnostic tests and their limitations are discussed in more detail by Greiner and Gardner ([#_ENREF_8 2000]).
Estimating specificity in uninfected populations
One special case of a gold standard comparison is for estimating test specificity in an uninfected population. In this case either historical information or other testing can be used to determine that a defined population is free of the disease of concern. This can be based on either a geographic region which is known to be free, or on intensive testing of a herd or herds over a period of time to provide a high level of confidence of freedom. If the population is assumed to be free, by definition all animals in the population are uninfected. Therefore, if a sample of animals from the population is tested with the new test, any positives are assumed to be false positives and the test specificity is estimated as the proportion of samples that test negatively.
For example, to evaluate the specificity of a new test for foot-and-mouth disease you could collect samples from an appropriate number of animals in a FMD-free country and use these as your reference panel.
Two drawbacks of this approach are: firstly that you cannot estimate sensitivity in this sample, since none of the animals are infected; and secondly that by using a defined (often geographically isolated) population there is a risk that specificity may be different in this population to what might be the case in the target population where the test is to be used.
Non-gold-standard methods
Non-gold-standard methods for test evaluation can often be used in situations where the traditional gold-standard approaches are not possible or feasible. These methods do not depend on determining the true infection status of each individual. Instead, they use statistical approaches to calculate the values of sensitivity and specificity that best fit the available data.
Non gold-standard test evaluation makes no explicit assumptions about the disease state of the animals tested and relies on statistical methods to determine the most likely values for test sensitivity and/or specificity
Although these methods don’t rely on a gold standard for comparison, they do depend on a number of important assumptions. Violation of these assumptions could render the resulting estimates invalid. Non-gold-standard methods for estimating sensitivity and specificity of diagnostic tests have been described in more detail by Hui and Walter ([#_ENREF_9 1980]), Staquet et al. ([#_ENREF_19 1981]) and Enøe et al. ([#_ENREF_4 2000]).
Available non-gold-standard methods include:
Maximum likelihood estimation
Maximum likelihood methods use standard statistical methods to estimate sensitivity and specificity of multiple tests from a comparison of the results of multiple tests applied to the same individuals in multiple populations with different prevalence levels ([#_ENREF_9 Hui and Walter, 1980]; [#_ENREF_4 Enøe et al., 2000]; [#_ENREF_15 Pouillot et al., 2002]). Key assumptions for this approach are:
- The tests are independent, conditional on disease status (the sensitivity [specificity] of one test is the same, regardless of the result of the other test, as discussed in more detail in the section on series and parallel interpretation of tests);
- Test sensitivity and specificity are constant across populations;
- The tests are compared in two or more populations with different prevalence between populations; and
- There are at least as many populations as there are tests being evaluated.
Bayesian estimation
Bayesian methods have been developed that allow the estimation of sensitivity and specificity of one or two tests that are compared in single or multiple populations ([#11 Joseph et al., 1995]; [#4 Enøe et al., 2000]; [#10 Johnson et al., 2001]; [#2 Branscum et al., 2005]). These methods allow incorporation of any prior knowledge on the likely sensitivity and specificity of the test(s) and of disease prevalence as probability distributions, expressing any uncertainty about the assumed prior values. Methods are also available for evaluation of correlated tests, but these require inclusion of additional tests and/or populations to ensure that the Bayesian model works properly ([#7 Georgiadis et al., 2003]).
Bayesian methods rely on the same assumptions as the maximum likelihood methods. In addition, Bayesian methods also assume that appropriate and reasonable distributions have been used for prior estimates for sensitivity and specificity of the tests being evaluated and prevalence in the population(s). For critical distributions where prior knowledge is lacking it may be appropriate to use an uninformative (uniform) prior distribution.
Comparison with a known reference test
Sensitivity and specificity can also be estimated by comparison with a reference test of known sensitivity and/or specificity ([#_ENREF_19 Staquet et al., 1981]). These methods cover a variety of circumstances, depending on whether sensitivity or specificity or both are known for the reference test. Key assumptions are conditional independence of tests, and that the sensitivity and/or specificity of the reference test is known.
In the special situation where the reference test is known to be close to 100% specific (for example culture or PCR-based tests), the sensitivity of the new test can be estimated in those animals that test positive to the reference test:
Se(new test) = Number positive to both tests / Total number positive to the comparison test
However, the specificity of the new test cannot be reliably estimated in this way, and will generally be under-estimated.
Estimation from routine testing data
Where a disease is rare, and truly infected animals can be eliminated from the data, it is possible to estimate test specificity from routine testing results, such as in a disease control program ([#17 Seiler, 1979]). In this situation, test-positives are routinely subject to follow-up, so that truly infected animals are identified and removed from the population. It is also possible to identify and exclude tests from known infected herds or flocks. Specificity can then be estimated as:
Sp = 1 - (Number of reactors / Total number tested)
In fact, this is an under-estimate of the true specificity, because there may be some unidentified but infected animals remaining in the data after exclusion of tests from known infected animals or herds/flocks.
For example: The flock-specificity of pooled faecal culture for the detection of ovine Johne's disease was estimated from laboratory testing records in New South Wales ([#18 Sergeant et al., 2002]). In this analysis, there were nine test-positive flocks out of 227 flocks eligible for inclusion in the analysis. After exclusion of results for seven known infected flocks, there were 2/220 flocks positive, resulting in an estimated minimum flock-specificity of 99.1% (95% Binomial CI: 96.9% - 99.9%). In fact one or both of these flocks could have been infected, and the true flock-specificity could be higher than the estimate of 99.1%.
Modelling approaches
Several novel approaches using modelling have also been used to estimate test sensitivity and/or specificity without having to rely on a comparison with either a gold standard or an alternative, independent test.
Mixture modelling
One approach to estimating test sensitivity and specificity in the absence of a gold standard is that of mixture population modelling. This approach is based on the assumption that the observed distribution of test results (for a test with a continuous outcome reading such as an ELISA) is actually a mixture of two frequency distributions, one for infected individuals and one for uninfected individuals.
Using mixture population modelling methods, it is possible to determine the theoretical probability distributions for uninfected and infected sub-populations that best fit the observed data, and from these distributions to estimate sensitivity and specificity for any cut-point.
For example, this approach was used to estimate sensitivity and specificity for ELISA for Toxoplasma gondii infection in Dutch sheep ([#14 Opsteegh et al., 2010]). ELISA results from 1,179 serum samples collected from sheep at slaughterhouses in the Netherlands were log transformed and normal distributions fitted to the infected and uninfected components. The resulting theoretical distributions allowed determination of a suitable cut-point with estimated sensitivity of 97.8% and specificity of 96.4%.
While this is a useful approach for estimating sensitivity and specificity in the absence of suitable comparative test data, it does depend on the assumptions that the test results follow the theoretical distributions calculated and that the sample tested is representative of the population at large. If the actual results deviate significantly from the theoretical distributions, or the sample is biased, estimates will also be biased.
Simulation modelling of longitudinal testing results
An alternative approach, using simulation modelling, has been used where no comparative test data was available, but results of repeated testing over time were available. In this example, the sensitivity of an ELISA for bovine Johne’s disease was estimated from repeated herd-testing results over a 10-year period using a simulation model. Age-specific data from up to 7 annual tests in 542 dairy herds were used to estimate ELISA sensitivity at the first-round test. The total number of infected animals present at the first test was estimated from the number of reactors detected at that test, plus the estimated number of animals that failed to react at that test, but reacted (or would have reacted if they had not died or been previously culled) at a subsequent test, based on reactor rates at subsequent tests. Reactor rates were adjusted for an assumed ELISA specificity of 99.8% to ensure estimates were not biased by imperfect ELISA specificity ([#_ENREF_12 Jubb et al., 2004]). Age-specific estimates of ELISA sensitivity ranged from 1.2% in 2-year-old cattle to 30.8% in 10-year-old cattle, with an overall age-weighted average of 13.5%.
This approach depends on the assumption that most JD-infected animals become infected at a young age, and that all animals that subsequently reacted to the ELISA were in fact infected at the time of the first test. If adult infection occurred in these animals the estimated sensitivity could have substantially under-estimated the true value.
References – diagnostic testing
Branscum, A. J., Gardner, I. A. & Johnson, W. O. 2005. Estimation of diagnostic-test semnsitivity and specificity through Bayesian modelling. Preventive Veterinary Medicine, 68:145-163.
Cicchetti, D. V. & Feinstein, A. R. 1990. High agreement but low kappa: II. Resolving the paradoxes. Journal-of-Clinical-Epidemiology, 43:551-558.
Enøe, C., Georgiadis, M. P. & Johnson, W. O. 2000. Estimation of sensitivity and specificity of diagnostic tests and disease prevalence when the true disease state is unknown. Preventive Veterinary Medicine, 45:61-81.
Everitt, R. S. 1989. Statistical Methods for Medical Investigation, New York, Oxford University Press.
Feinstein, A. R. & Cicchetti, D. V. 1990. High agreement but low kappa: I. The problems of two paradoxes. [see comments.]. Journal of Clinical Epidemiology., 43:43-9.
Georgiadis, M. P., Johnson, W. O., Singh, R. & Gardner, I. A. 2003. Correlation-adjusted estimation of sensitivity and specificity of two diagnostic tests. Applied statistics, 52:63-76.
Greiner, M. & Gardner, I. A. 2000. Epidemiologic issues in the validation of veterinary diagnostic tests. Preventive Veterinary Medicine, 45:3-22.
Hui, S. L. & Walter, S. D. 1980. Estimating the error rates of diagnostic tests. Biometrics, 36:167-171.
Johnson, W. O., Gastwirth, J. L. & Pearson, L. M. 2001. Screening without a "gold standard": the Hui-Walter paradigm revisited. American Journal of Epidemiology, 153:921-924.
Joseph, L., Gyorkos, T. W. & Coupal, L. 1995. Bayesian estimation of disease prevalence and the parameters of diagnostic tests in the absence of a gold standard. American-Journal-of-Epidemiology, 141:263-272.
Jubb, T. F., Sergeant, E. S. G., Callinan, A. P. L. & Galvin, J. W. 2004. Estimate of sensitivity of an ELISA used to detect Johne's disease in Victorian dairy herds. Australian Veterinary Journal, 82:569-573.
Martin, S. W., Shoukri, M. & Thorburn, M. A. 1992. Evaluating the health status of herds based on tests applied to individuals. Preventive-Veterinary-Medicine, 14:33-43.
Opsteegh, M., Teunis, P., Mensink, M., Zuchner, L., Titilincu, A., Langelaar, M. & van der Giessen, J. 2010. Evaluation of ELISA test characteristics and estimation of Toxoplasma gondii seroprevalence in Dutch sheep using mixture models. Preventive Veterinary Medicine.
Pouillot, R., Gerbier, G. & Gardner, I. A. 2002. "TAGS", a program for the evaluation of test accuracy in the absence of a gold standard. Preventive Veterinary Medicine, 53:67-81.
Rogan, W. J. & Gladen, B. 1978. Estimating prevalence from the results of a screening test. American Journal of Epidemiology, 107:71-76.
Seiler, R. J. 1979. The non-diseased reactor: considerations on the interpretation of screening test results. Veterinary-Record, 105:226-228.
Sergeant, E. S. G., Whittington, R. J. & More, S. J. 2002. Sensitivity and specificity of pooled faecal culture and serology as flock-screening tests for detection of ovine paratuberculosis in Australia. Preventive-Veterinary-Medicine, 52:199-211.
Staquet, M., Rozencweig, M., Lee, Y. J. & Muggia, F. M. 1981. Methodology for the assessment of new dichotomous diagnostic tests. Journal-of-Chronic-Diseases, 34:599-610.